三体问题新突破

    牛顿的引力理论正确预测两个互相吸引的天体(比如太阳和地球)的运动规律——它们的轨道基本是椭圆形。但如果有3个天体(比如太阳、地球和月球)互相作用，它们的运行轨道有什么规律?这就是著名的“三体问题”。最近，有两位科学家一口气找到了13族新的周期性特解，震惊了科学界。

    “三体问题”的提出可以追溯到17世纪80年代，当时英国物理学家、数学家艾萨克·牛顿运用他的引力理论正确预测两个互相吸引的天体(比如太阳和地球)的运动规律——它们的轨道基本是椭圆形。但如果有3个天体，比如太阳、地球和月球相互作用，它们的运行轨道是什么样的?牛顿没能给出通用的特解答案。

    简单地说，“三体问题”就是探讨3个质量、初始位置和初始速度都为任意的可视为质点的天体，在相互之间万有引力的作用下的运动规律问题。

    随后的200多年中，科学家们为解决这个问题绞尽脑汁，直到1887年德国数学家、天文学家海因里希·布伦斯指出，寻找三体问题的通解注定是无用功，只在特定条件下成立的特解才可能存在。

    1889年，法国数学家、天体力学家亨利·庞加莱将复杂的三体问题简化成了所谓的“限制性三体问题”。但他发现，即使对简化了的限制性三体问题，在同宿轨道或者异宿轨道附近，解的形态会非常复杂，以至于对于给定的初始条件，几乎没有办法预测当时间趋于无穷时，这个轨道的最终命运。而这种对于轨道的长时间行为的不确定性，这也就是我们目前称之为“混沌”(chaos)的现象。现在人们知道，通常情况下三体问题的解是非周期性的。

    要发现三体问题的周期性特解绝非易事——自“三体问题”被确认以来的300多年中，人们只找到了3族周期性特解。

    法国数学家、物理学家约瑟夫·拉格朗日和瑞士数学家、物理学家莱昂哈德·欧拉在18世纪得到了一些结果;20世纪70年代，美国数学家罗杰·布鲁克和法国天文学家米歇尔·赫农借助计算机又得到了更多的结果;1993年，美国数学家、物理学家克里斯·摩尔发现一种奇特现象——特解中3个天体的运动似在一条“8”字形的轨道上互相追逐。上述所有这些被发现的特解可以被归结为下面3族:拉格朗日-欧拉族、布鲁克-赫农族和“8”字形族。拉格朗日-欧拉族的解比较简单，就是三个天体等间距地在圆轨道上运动，就像旋转木马那样。布鲁克-赫农族的解比较复杂，两个天体在里面横冲直撞，第三个天体在它们外围做环绕运动。

    要知道，发现新的特解不是一件容易的事:三个天体在空间中的分布可以有无穷多种情况，必须找到合适的初始条件——起始点、速度等，才能使系统在运动一段时间之后回到初始状态，即进行周期性的运动。

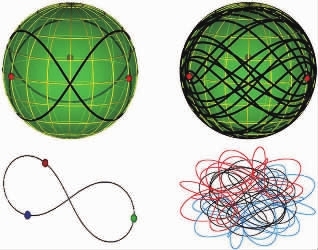
    现在，科学家们有了新突破。塞尔维亚物理学家米洛万·舒瓦科夫和迪米特拉·什诺维奇发现了新的13族特解。他们在著名学术期刊《物理评论快报》上发表了论文，描述了他们的寻找方法:运用计算机模拟，先从一个已知的特解开始，然后不断地对其初始条件进行微小的调整，直到新的运动模式被发现。这13族特解非常复杂，在抽象空间“形状球”中，就像一个松散的线团。

    三体问题特解的族数被扩充到了16族。这一新发现令科学界欢欣鼓舞。多年来一直从事三体问题研究的美国科学家罗伯特·范德贝说，“我非常喜欢这一成果”。另一位美国科学家理查德·蒙哥马利说:“这些结果非常美妙，而且描述非常精彩。”中国科学家周海中表示，他们的成果加深了人们对天体运动的了解，促进了天体力学和数学物理的进一步发展，尤其是对人们研究太空火箭轨道和双星演化很有帮助。

    (作者为日本东京大学博士后)